Search the Community

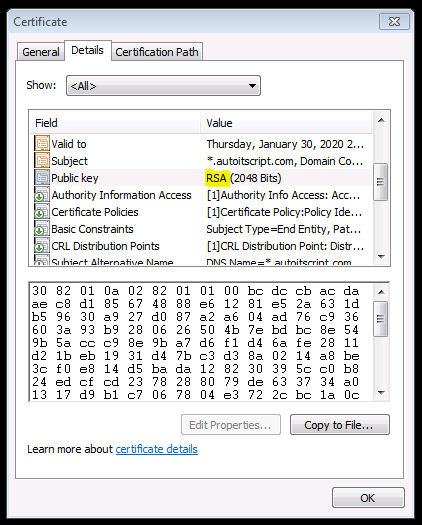
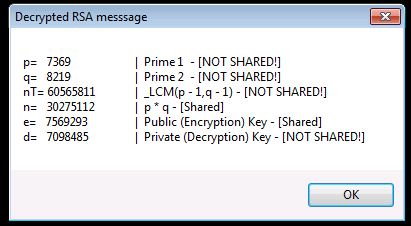
I found this article and enjoyed it so much I had play with some code since the numbers are small enough. https://thatsmaths.com/2016/08/11/a-toy-example-of-rsa-encryption/ Standard Encryption's vs RSA Encryption (Public Key Encryption) Fundamental Differences If you read that and couldn't immediately clarify the difference then let me blow your mind because its simple: STANDARD ENCRYPTION'S: ORIGINAL_DATA + Password(or KEY) = Encrypted DATA Then to decrypt -> Encrypted DATA + (SAME Password(or SAME KEY)) = ORIGINAL_DATA RSA: ORIGINAL_DATA + Password(or PUBLIC_KEY) = Encrypted DATA Then to decrypt -> Encrypted DATA + (DIFFERENT Password(or PRIVATE_KEY)) = ORIGINAL_DATA Are we all caught up? Did the colors help? I think they did That's crazy right? Don't answer. It is. And crazier its used EVERY TIME we make a secure connection to a server over the internet. But here's the craziest part to me that I recently got clarity on from the toy example and that is the simplicity of this very very very very important algorithm that has yet to be cracked (fingers crossed): Mod($vData ^ $key, $n) So ya. That's it. That's the magic algorithm. 3 values. Oh and $n is also a shared known value that will be in the certificate with the public key that your browser reads when it makes a connection: That's just mind blowing to me so couldn't resist getting something going in AUT. After playing with this code, I got a much better understanding of how its not just that algorithm that makes this whole thing possible. The numbers that we pick to form the public key and n are just as important and also how important it is to be random! Let me know if you have any problems. Enjoy! #include <array.au3> _Toy_RSA_Example() ;https://thatsmaths.com/2016/08/11/a-toy-example-of-rsa-encryption/ Func _Toy_RSA_Example() Local $p, $q, $n, $nT, $e, $d Local $aPublicKeys, $aCrypt, $sDecrypt, $sMsg ;Pick two random primes (they will be between 1000-10000) $p = _GetRandomPrime() $q = _GetRandomPrime() $sMsg = 'p= %i \t\t| Prime 1 - [NOT SHARED!]\nq= %i \t\t| Prime 2 - [NOT SHARED!]\n' ;Calculate lowest common multiple $nT = _LCM($p - 1, $q - 1) $sMsg &= 'nT= %i \t| _LCM(p - 1,q - 1) - [NOT SHARED!]\n' ;Calculate n. This is a shared number $n = $p * $q $sMsg &= 'n= %i \t| p * q - [Shared]\n' ;Get a small random list of possible public keys to pick from. Only searching for 100ms $aPublicKeys = _GetPublicKeys($nT) _ArrayDisplay($aPublicKeys, "Possible Public Keys Found") ;Pick a random public (encryption) key from array $e = $aPublicKeys[Random(1, $aPublicKeys[0], 1)] $sMsg &= 'e= %i \t| Public (Encryption) Key - [Shared]\n' ;Generate our private (decryption) key $d = _GetPrivateKey($e, $nT) $sMsg &= 'd= %i \t| Private (Decryption) Key - [NOT SHARED!]\n' ;format our msg (rsa details) to encrypt $sMsg = StringFormat($sMsg, $p, $q, $nT, $n, $e, $d) ;encrypt message $aCrypt = _RSA($sMsg, $e, $n) _ArrayDisplay($aCrypt, 'Encrypted RSA messsage') ;Decrypt array back $sDecrypt = _RSA($aCrypt, $d, $n) MsgBox(0, 'Decrypted RSA messsage', $sDecrypt) EndFunc ;==>_Toy_RSA_Example ;Function will perfrom Mod($v ^ $key, $n) on each char/element. ;Excepts Arrays or Strings. If input is array a string is returned and vice versa. Func _RSA($vDat, $key, $n) Local $bIsStr = IsString($vDat) If $bIsStr Then $vDat = StringToASCIIArray($vDat) For $i = 0 To UBound($vDat) - 1 $vDat[$i] = _Modular($vDat[$i], $key, $n) Next Return $bIsStr ? $vDat : StringFromASCIIArray($vDat) EndFunc ;==>_RSA ;algorithm is from the book "Discrete Mathematics and Its Applications 5th Edition" by Kenneth H. Rosen. Func _Modular($iBase, $iExp, $iMod) ; Mod($v ^ $key, $n) Local $iPower = Mod($iBase, $iMod) Local $x = 1 For $i = 0 To (4 * 8) - 1 If BitAND(0x00000001, BitShift($iExp, $i)) Then $x = Mod(($x * $iPower), $iMod) EndIf $iPower = Mod(($iPower * $iPower), $iMod) Next Return $x EndFunc ;==>_Modular ;Generate a "random" list of possible valid public keys to choose from based on $nT Func _GetPublicKeys($nT, $iMs = 100) Do Local $aKeys[10000] = [0], $iTime = TimerInit() Local $i = (Mod(@SEC, 2) ? Int($nT / 2) : Int($nT / 4)) ; randomize where we start Do If _IsPrime($i) And _IsCoPrime($i, $nT) Then $aKeys[0] += 1 $aKeys[$aKeys[0]] = $i EndIf $i += (Mod(@MSEC, 2) ? 1 : 100) ; randomize step size Until ($i >= ($nT - 1)) Or (TimerDiff($iTime) > $iMs) ReDim $aKeys[$aKeys[0] + 1] Until $aKeys[0] > 5 ; Ive seen 200+ returned sometimes and 0 on others. Make sure we have at least a few choices Return $aKeys EndFunc ;==>_GetPublicKeys ;https://www.geeksforgeeks.org/multiplicative-inverse-under-modulo-m/ - _ModInverse(a,m) Func _GetPrivateKey($a, $m) If ($m = 1) Then Return 0 ; Local $t, $q, $y = 0, $x = 1, $m0 = $m While ($a > 1) $q = Int($a / $m) ;q is quotient $t = $m ; $m = Mod($a, $m) ;m is remainder now, process same as Euclid's algo $a = $t ; $t = $y ; $y = $x - $q * $y ;Update y and x $x = $t ; WEnd Return $x < 0 ? $x + $m0 : $x EndFunc ;==>_GetPrivateKey ;Pick the next nearest prime from a random number (or number you cho0se) Func _GetRandomPrime($iStart = Default) Local $iPrime = ($iStart = Default ? Random(1000, 10000, 1) : $iStart) Do $iPrime += 1 Until _IsPrime($iPrime) Return $iPrime EndFunc ;==>_GetRandomPrime #Region Math Functions Func _IsPrime($n) For $i = 2 To (Int($n ^ 0.5) + 1) If Mod($n, $i) = 0 Then Return False Next Return True EndFunc ;==>_IsPrime Func _IsCoPrime($a, $b) Return _GCD($a, $b) = 1 EndFunc ;==>_IsCoPrime Func _GCD($iX, $iY) Local $iM While 1 $iM = Mod($iX, $iY) If $iM = 0 Then Return $iY $iX = $iY $iY = $iM WEnd EndFunc ;==>_GCD Func _LCM($iX, $iY) Return ($iX * $iY) / _GCD($iX, $iY) EndFunc ;==>_LCM #EndRegion Math Functions You should get a message box displaying the decrypted message with details of the values used: rsa.au3